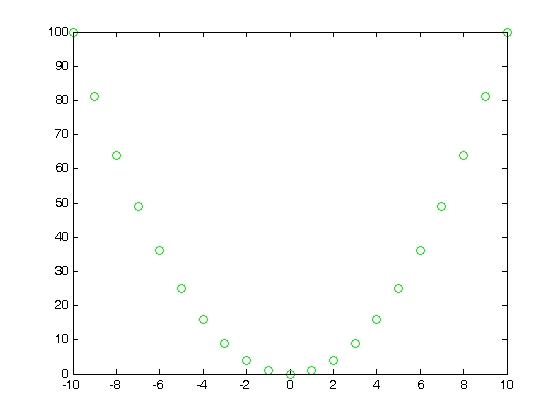
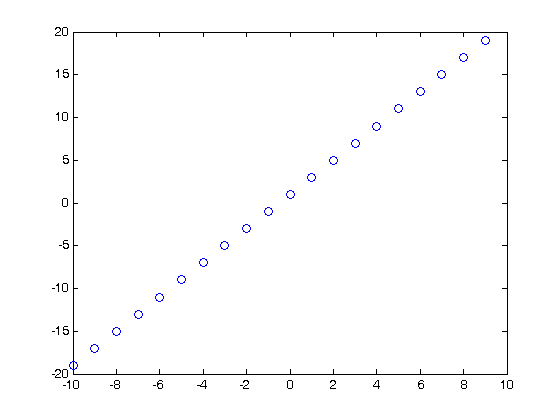
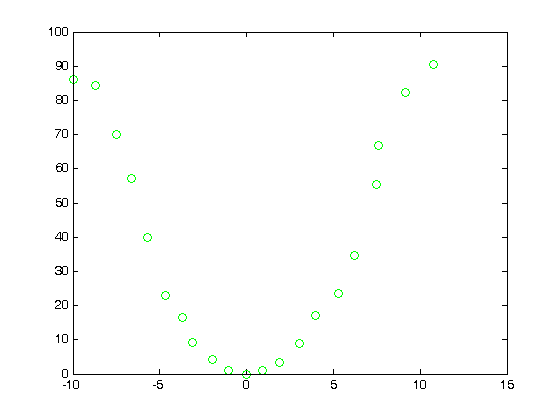
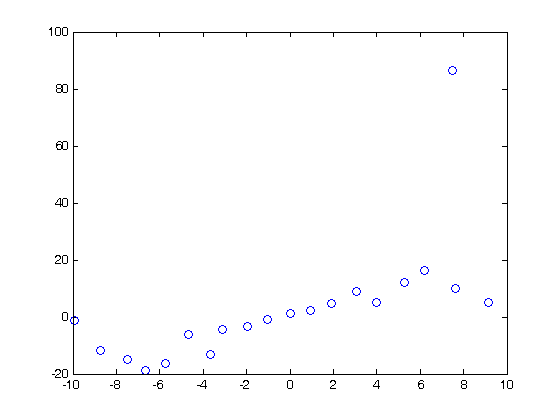
% Jake Bobowski % June 10, 2016 % Created using MATLAB R2014a % Clear all variable assignments. clearvars % In this MATLAB script we attempt to evaluate numberical derivatives on a % list of data. % First, we introduce the 'diff' function. diff(x) will take list x and % create a new list whose elements are equal to the difference between % adjacent elements in x. For example, let's make x a list from -10 to 10 in % steps of 1. x = (-10:1:10) dx = diff(x) % In this case, dx is a list of ones. Notice that, because it is determined % from a difference, dx is one element shorter that x. length(x) length(dx) % Now let's make y = x^2 and plot y vs x. The result is clearly a % quadratic. y = x.^2; plot(x,y, 'go') % To evaluate the derivative of y with respect to x, we need to determine % the change in y over the change in x. dydx = diff(y)./diff(x) % We should expect dydx vs x to be a straigt line of slope 2. To generate % the plot, remember that we have to reduce the length of x by 1. x1 = x(1:length(x)-1); p = polyfit(x1,dydx,1) figure() plot(x1,dydx,'o') yfit = polyval(p,x1); % Notice from the fit that the slope is indeed 2, but the y-intercept is 1 % instead of the expected zero. This is an artifact of taking derivatives % of a discrete set of the data. We can improve our results if we reduced % the spacing between the x data. % Just for fun, let's add some noise to our data. Let's suppose that the % uncertainty in x is 10% and that dy = 2*x*dx. rand() generates a random % number uniformly distributed between 0 and 1. You can confirm for % yourself that a + (b - a)*rand() generates a random number between a and % b. yN = zeros(1,length(x)); for k = 1:length(x) xN(k) = x(k) + 0.1*x(k)*(-1 + (1 - (-1))*rand()); yN(k) = x(k)^2 + 2*x(k)*0.1*x(k)*(-1 + (1 - (-1))*rand()); end figure() plot(xN,yN,'o'); dyNdx = diff(yN)./diff(xN); plot(xN, yN,'go'); xN1 = xN(1:length(xN)-1); figure() plot(xN1, dyNdx,'o'); p = polyfit(x1,dyNdx,1) % As you might have anticipated, taking the ratio of the differences between a % pair of noisey datasets results in even more fluctuations. Obtaining % clear derivatives from discrete datasets requires precision measurements.
x =
Columns 1 through 13
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2
Columns 14 through 21
3 4 5 6 7 8 9 10
dx =
Columns 1 through 13
1 1 1 1 1 1 1 1 1 1 1 1 1
Columns 14 through 20
1 1 1 1 1 1 1
ans =
21
ans =
20
dydx =
Columns 1 through 13
-19 -17 -15 -13 -11 -9 -7 -5 -3 -1 1 3 5
Columns 14 through 20
7 9 11 13 15 17 19
p =
2.0000 1.0000
p =
2.3370 4.2110