Mathematical Modelling in Spatial Ecology
Natural landscapes are continually subject to fragmentation due to natural causes - fire, disease, storms, etc. Human activity however, is fragmenting habitat more permanently, and at a far greater rate. The survival of animals living in these habitats depends on their ability to cope with fragmentation. On the flip side, we have species who have successfully managed to proliferate in non-native habitats, and these biological invasions carry an enormous economic cost. Successful invaders become pests without natural enemies, and so can decimate crops, choke up harbours or destroy forests to name just a few examples.
To understand what habitat fragmentation a threatened species can survive, or how to control an invasive species, we need to know how individuals and populations disperse in the spatial landscape. It is challenging and costly however, to track moving individuals in sufficient numbers over sufficiently large distances to gain an accurate picture of their dispersal behaviour. Mathematical modelling is an important tool in this research.
In collaboration with experimentalists, I am developing and investigating mathematical models of organisms interacting with and moving through their spatial habitat. My models describe the population dynamics and spatial movement of these organisms and the heterogeneous landscape in which they live. I am interested in understanding how the population dynamics of these organisms are affected by habitat fragmentation caused by roads, harvesting, urban development, and other factors. Through these projects, I am seeking to uncover basic principles regarding how population dynamics are influenced by spatial heterogeneity.
Modelling the Dispersal Behaviour of Wild and Sterile Codling Moths
The Codling moth is a major pest for apple and pear growers worldwide. It originated in Asia Minor, and has migrated across all the temperate regions of the world, with the exception of Japan and part of mainland Asia. The traditional method of control involves extensive use of chemical sprays. As we become more aware of the environmental and health issues surrounding these sprays however, there is growing interest in finding alternative control methods. In recent years, a Sterile Insect Technique (SIT) has been developed and is in use in the Okanagan Valley. Codling moths are mass-reared in a facility, where at adulthood they are sterilised and then released in large numbers in orchards. These sterile moths mate with the wild moths, with the result that the females lay unfertilized eggs which therefore produce no offspring.
Theoretical calculations have shown that it should be possible to eradicate the local population of Codling moths using the SIT. Unfortunately, though the wild population is decreasing, it is proving more resilient than expected. To understand why this is so, and to make the use of the SIT more effective, we need a detailed understanding of how the moths disperse in a heterogeneous landscape.
I am developing and studying two different models for codling moth dispersal. One is a continuous partial differential equation model which is useful for asking population-level questions and analysis at the landscape level. The other model is an individual-based (IB) simulation model which allows us to study moth behaviour in detail at the level of an orchard. Kyle Newton has been doing most of the model development of the IB model.
This work is being done in collaboration with Dr. Howard Thistlewood and Dr. Gary Judd, entomologists from the Pacific Agri-Food Research Centre in Summerland. We are using data they have collected and are collecting from sites in the Okanagan-Similkameen Valley.

A photograph of one of the experimental study sites in the Okanagan-Similkameen Valley.
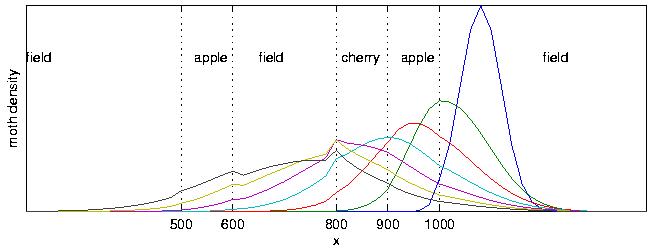
A one-dimensional simulation from the continuous model showing the dispersal of sterile male moths in the presence of ambient wind across a heterogeneous landscape. In this simulation, the wind direction is left to right, and the moths are released from a point in a field to the right of the rightmost apple orchard.
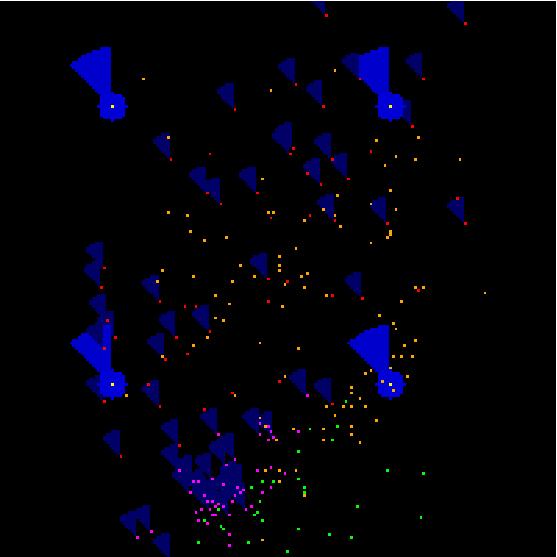
A snapshot of the Individual-Based model simulation. White dots are traps and light blue areas are areas where moths can detect pheromone released by these traps. Red and pink dots are sterile and wild female moths respectively, and dark blue areas are areas where moths can detect pheromone released by the female moths. Orange dots and green dots are sterile and wild male moths respectively. The angle at which each triangular pheromone plume is pointing depends on the wind direction, as pheromone is blown downwind. In this snapshot the wind is coming from the bottom right hand corner of the picture, and blowing toward the top left hand corner.
Modelling the Recolonization of Second-Growth Forest Stands by the North American red squirrel, Tamiasciurus hudsonicus
The North American red squirrel , Tamiasciurus hudsonicus, is a small, tree-dwelling rodent that ranges throughout much of the coniferous forests in North America. It is a very territorial squirrel, with each adult occupying a defined territory within which they have enough food and shelter for their own survival. Adults generally claim a territory for life, defending it with regular vocalisations. The main food source for red squirrels is the seeds of pine and fir cones, and winter shelter (and escape from predators) is found in a pile of discarded bracts and other debris called a midden. These middens are passed on from one squirrel to another and so a well-established midden has a network of tunnels, insulated by the bract pile, which provide food storage and warm winter shelter.
Karl Larsen has been studying squirrel populations in mature and second-growth forest stands. He is interested in understanding the patterns and mechanisms behind natal dispersal, which is the movement and settlement of juvenile animals. He has been examining the dispersal of these animals at two scales: the individual level (intense monitoring of individual dispersers) and from a broader landscape perspective (looking at population responses to different-ages and qualities of habitat). His research has shown that there are important differences between the mature and second-growth forest stands from the point of view of red squirrel population dynamics. There are a couple of obvious reasons for this. First, when an area of forest is harvested, squirrels can no longer survive in territories there since the cone-producing trees are largely removed. Second, in any season other than winter, the heavy machinery used in logging destroys any middens in the harvested area. Thus, recolonization of the area can't occur until a cone-producing forest is once again present, and survival of squirrels will remain low until there has been sufficient time to build sufficiently large middens. Other factors may also contribute to low squirrel survival.
The ongoing turnover of forest stands (by harvesting, or by wildfire), creates a shifting mosaic of habitat, composed of both suitable and unsuitable patches for the squirrels. We are using mathematical models, in combination with field study, to help us understand how the juxtaposition and relative amounts of different forest-age patches impact animal populations, such as red squirrels

The North American red squirrel, Tamiasciurus hudsonicus (image from the University of Michigan Museum of Zoology).
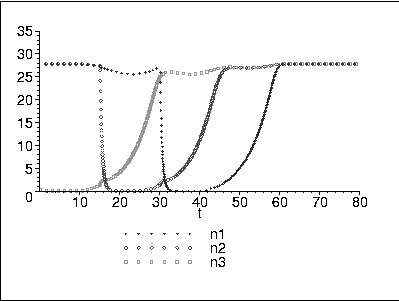
A one-dimensional simulation showing the timeline for population recovery in harvested stands. When each stand is clearcut, the population there goes to zero. Once the second-growth forest starts producing cones, the population in the harvested patch can increase.
Modelling the Predator-Prey Dynamics of Southern Snowshoe Hare Populations
With Dr Karen Hodges, CRC chair in Conservation Biology at UBC Okanagan, I have recently begun modelling the population dynamics of southern snowshoe hare populations and its major predators which include the endangered Canada lynx . These populations differ from northern ones in at least three important ways: their habitats are more fragmented; they are complicated by more hare predators; and they do not appear to undergo the 10-year population cycles which are so distinctive in the north. Our goal is to build a deterministic mathematical model of the southern hare and lynx community, including other hare predators, and use the model to test various hypotheses about these populations.
Our model includes equations for adult and juvenile hares, four important predators (lynx, coyote, great horned owl, goshawk) and a general equation for all other predators. Habitat quality is a parameter of the model, and is allowed to vary spatially. This will make model development and analysis particularly challenging.
One of the key model components is the manner in which we describe lynx movement in a spatially fragmented habitat. It has been observed that lynx move quickly (in straight lines) across low-quality or harvested forest habitat, and then apparently search randomly in patches of high quality habitat. We will thus be modelling predator movement as both random and directed motion, with the former (latter) decreasing (increasing) as habitat fragmentation increases. The directed motion must allow lynx to visually orient toward high quality habitat.
Modelling the Swimming Behaviour of the Nematode
With Dr. C.E. Jordan (University of Colorado, Boulder) and Dr. L.J. Fauci (Tulane University) I have been working on a study of the swimming motion of the nematode. We are interested in understanding how the internal muscle mechanics of the nematode interact with the fluid dynamics of the surrounding fluid to produce the characteristic swimming motion of the organism.
Our modelling problem thus has two parts: the motion of the nematode musculature, and the motion of the surrounding fluid. We are using ordinary differential equations to describe the muscle mechanics, incorporating extensive quantitative experimental results on the behaviour of nematode muscle and swimming nematodes. The mechanics of the surrounding fluid are described by the Navier-Stokes equations, which are well-studied. We are using a standard solver for the full Navier-Stokes equations.
In order to computationally transfer information between the two parts of the model - the nematode and the surrounding fluid - we use the immersed boundary method developed by Charles Peskin . The project and immersed boundary method are explained in more detail in a talk I gave in Montreal in 2008.
I have a few Movies made of our 2-d computational nematode available. Justin Hebert is developing a 3-d model.